Archive for Oktober 2015
Distribusi Frekuensi
Definisi Distribusi Frekuensi
Jenis Distribusi Frekuensi
Tujuan Distribusi Frekuensi : untuk mengatur data mentah (belum dikelompokan) ke dalam bentuk yang rapi tanpa mengurangi inti informasi yang ada, Data menjadi informatif dan mudah dipahami.
Ditinjau dari jenisnya : Numerik : pengelompokan data berdasarkan angka – angka tertentu, biasanya sajikan dengan grafik histogram. Kategorikal : pengelompokan data berdasarkan kategori – kategori tertentu, biasanya disajikan dengan grafik batang, lingkaran dan gambar.
Ditinjau dari nyata tidaknya frekuensi : Absolut, jumlah bilangan yang menyatakan banyaknya data pada suatu kelompok tertentu. Relatif, juga dinamakan tabel persentase.
Ditinjau dari kesatuannya : Satuan, Kumulatif.
Data yang diolah merupakan suatu deret hitung yang berdiri sendiri.
Jenis Tabel Distribusi Frekuensi:
Langkah-langkah menjawab soal di atas seperti ini :
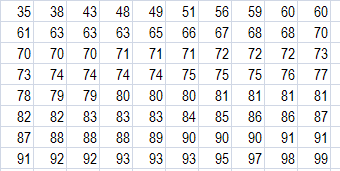
Langkah 1 : Urutkan dari yang terkecil hingga yang terbesar guna memudahkan dalam melakukan pernghitungan.
jika:
- Merupakan penyusunan data ke dalam kelas – kelas tertentu dimana setiap indiIvidu/item hanya termasuk kedalam salah satu kelas tertentu
- Pengelompokan data ke dalam beberapa kategori yang menunjukan banyaknya data dalam setiap kategori dan setiap data tidak dapat dimasukan ke dalam dua atau lebih kategori.
- Distribusi Frekuensi adalah penyusunan data dalam kelas-kelas interval. (Kuswanto,2006).
- Distribusi Frekuensi adalah membuat uraian dari suatu hasil penelitian dan menyajikan hasil penelitian tersebut dalam bentuk yang baik, yakni bentuk stastistik popular yang sederhana sehingga kita dapat lebih mudah mendapat gambaran tentang situasi hasil penelitian. (Djarwanto,1982).
- Distribusi Frekuensi atau Tabel Frekuensi adalah suatu tabel yang banyaknya kejadian atau frekuensi (cases) didistribusikan ke dalam kelompok-kelompok (kelas-kelas) yang berbeda. (Budiyuwono,1987).
Jenis Distribusi Frekuensi
Tujuan Distribusi Frekuensi : untuk mengatur data mentah (belum dikelompokan) ke dalam bentuk yang rapi tanpa mengurangi inti informasi yang ada, Data menjadi informatif dan mudah dipahami.
Ditinjau dari jenisnya : Numerik : pengelompokan data berdasarkan angka – angka tertentu, biasanya sajikan dengan grafik histogram. Kategorikal : pengelompokan data berdasarkan kategori – kategori tertentu, biasanya disajikan dengan grafik batang, lingkaran dan gambar.
Ditinjau dari nyata tidaknya frekuensi : Absolut, jumlah bilangan yang menyatakan banyaknya data pada suatu kelompok tertentu. Relatif, juga dinamakan tabel persentase.
Ditinjau dari kesatuannya : Satuan, Kumulatif.
Data yang diolah merupakan suatu deret hitung yang berdiri sendiri.
Jenis Tabel Distribusi Frekuensi:
- Tabel distribusi frekuensi data tunggal, menyajikan frekuensi data yang tidak dikelompokkan.
- Tabel distribusi frekuensi data kelompok, menyajikan pencaran frekuensi data yang kelompokkan.
- Tabel distribusi frekuensi kumulatif, menyajikan frekuensi yang datanya selalu ditambahkan.
- Tabel distribusi frekuensi relative, menyajikan data frekuensi yang bukan sebenarnya, misalnya dalam bentuk persen.
Langkah-langkah menjawab soal di atas seperti ini :
Langkah 1 : Urutkan dari yang terkecil hingga yang terbesar guna memudahkan dalam melakukan pernghitungan.

Kemudian tentukan
Nilai Max & Nilai Min, untuk membuat jangkauan (Range).
Min =
35
Max =
99
Range =
99-35 = 64
Langkah 2
: Sebenarnya tidak ada aturan pasti, untuk mudahnya bisa
menggunakan aturan Sturges.
Aturan Sturges K = 1 +
3,322 log n atau K = 1+3,3 log n
K = banyaknya
kelas
n = banyaknya jumlah
data observasi
Banyaknya data atau n
= 80 maka...
K
= 1 + 3,3 log 80
= 1 + 3,3 (1,903)
= 1 + 6,279
= 7,279 ≈ 7
= 1 + 6,279
= 7,279 ≈ 7
Langkah 3
: Panjang/Lebar Kelas (Interval).
Interval adalah selisih batas atas
dan batas bawah dari suatu kategori.
jika:
Panjang Kelas P = J/K
= Xn-X1/K
K = banyaknya kelas
Xn = nilai observasi
terbesar
X1 = nilai observasi
terkecil
Maka :
P = 99-35/7
=64/7
= 9,143 ≈ 9
P = 99-35/7
=64/7
= 9,143 ≈ 9
Langkah 4 : Tabulasi
dan Tabel Frekuensi.
Batas kelas
: Nilai terendah dan tertinggi
Batas kelas dalam
suatu interval kelas terdiri dari dua macam :
·
Batas kelas bawah – lower class limit, Nilai teredah
dalam suati interval kelas.
·
Batas kelas atas – upper class limit, Nilai teringgi
dalam suatu interval kelas.
Pada tabel di atas, 44
merupakan nilai tertinggi kelas ke 1, dan 45 merupakan nilai terendah kelas ke
2. Begitupun seterusnya.
Nilai tengah
: Tanda atau perinci dari suatu interval kelas dan merupakan suatu angka
yang dapat dianggap mewakili suatu interval kelas. Nilai tengah kelas,
kelasnya berada di tengah-tengah pada setiap interval kelas.
Nilai
tengah kelas 1 : (35+44)/2 = 39,5
Nilai
tengah kelas 2 : (45+54)/2 = 49,5
Nilai
tengah kelas 3 : (55+64)/2 = 59,5
Dst.
Nilai tepi kelas
: Nilai batas antara kelas yang memisahkan nilai antara kelas satu dengan
kelas lainnya. Penjumlahan nilai atas kelas dengan nilai bawah kelas
diantaranya dan di bagi dua.
Nilai
tepi kelas 2 : (44+45)/2 = 44,5
Nilai tepi
kelas 3 : (54+55)/2 = 54,5
Nilai
tepi kelas 4 : (64+65)/2 = 64,5
Dst.
Distribusi Frekuensi
Absolut & Relatif :
Absolut : Jumlah
bilangan yang menyatakan banyaknya data pada suatu kelompok tertentu.
Relatif : Jumlah
persentase yang menyatakan banyaknya data pada suatu kelompok tertentu.
Frekuensi setiap kelas dibandingkan dengan frekuensi total. Tujuannya adalah
untuk memudahkan membaca data secara tepat dan tidak kehilangan makna dari
kandungan data.
Frekuensi Relatif =
Frekuensi Kelas/Jumlah Kelas x 100
Pada tebel diatas,
Frek.
Relatif kelas 1 : (3/80)x100 = 3,75
Frek.
Relatif kelas 2 : (3/80)x100 = 3,75
Frek.
Relatif kelas 3 : (8/80)x100 = 10
Frek.
Relatif kelas 4 : (21/80)x100 = 26,25
Dst
Distribusi Frekuensi
Satuan & Kumulatif
·
Distribusi frekuensi satuan : frekuensi yang
menunjukkan berapa banyak data pada kelompok tertentu.
·
Distribusi frekuensi kumulatif : distribusi frekuensi
yang menunjukkan jumlah frekuensi pada sekelompok nilai tertentu, mulai dari
kelompok sebelumnya sampai dengan kelompok tersebut.
·
Frekuensi kumulatif kurang dari : penjumlahan dari
mulai frekuensi terendah sampai kelas tertinggi dan jumlah akhirnya merupakan
jumlah data (n).
·
Frekuensi kumulatif lebih dari : pengurangan dari
jumlah data (n) dengan frekuensi setiap kelas dimulai dari kelas terendah dan
jumlah akhirnya adalah nol.
Grafik
Histogram :
Histogram merupakan
diagram balok. Histogram menghubungkan antara tepi kelas interval dengan
pada sumbu horizontal (X) dan frekuensi setiap kelas pada sumbu vertikal (Y).
Grafik
Polygon :
Menggunakan
garis yang mengubungkan titik – titik yang merupakan koordinat antara
nilai tengah kelas dengan jumlah frekuensi pada kelas tersebut.
Kurva
Ogif / Ogive :
Merupkan diagram garis yang menunjukan kombinasi antara
interval kelas dengan frekuensi kumulatif.